Масштабируемость и устойчивость
Чтобы продемонстрировать масштабируемость своего подхода, мы исследовали влияние на производительность системы (i) увеличения числа разделов и (ii) роста размера и сложности базы данных.
Табл. 1. Размеры графов.

На всех стадиях работы нашей системы, за исключением фазы разделения графа, производительность, по существу, не зависит от числа разделов и линейно возрастает в зависимости от размеров базы данных и трассы рабочей нагрузки. Поэтому чтобы продемонстрировать масштабируемость мы фокусируемся на производительности фазы разделения графа. Для этого эксперимента мы использовали три графа, характеристики которых приведены в табл. 1.
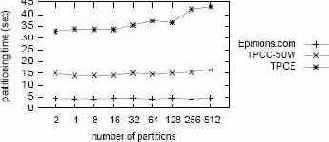
Рис. 5. Масштабируемость реализации разделения графов METIS при росте числа разделов и размеров графа.
На рис. 5 показано время работы последовательной реализации алгоритма разделения графов kmetis при возрастании числа разделов (детали экспериментальной установки см. в Приложении A). Стоимость разделения немного повышается при возрастании числа разделов. Рост размера графа оказывает гораздо более сильное воздействие на время выполнения (оно увеличивается почти линейно в зависимости от роста числа дуг), что оправдывает наши усилия на сокращение размеров графов на основе эвристик, представленных в подразделе 5.1.
Наиболее важной эвристикой для сокращения размеров графов является взятие образцов (sampling). Трудно точно сказать, до какого уровня можно довести взятие образцов при построении графа, чтобы с его помощью все еще можно было получать хорошую схему разделения базы данных. Однако наши эксперименты свидетельствуют о том, что Schism производит хорошие результаты даже при работе с небольшим образцом базы данных. Например, для TPC-C с двумя складами образца, состоящего из одного процента вершин и дуг полного графа, нам хватило для того, чтобы произвести такой же результат, что и при разделении вручную. Качественный анализ наших экспериментов показывает, что минимально требуемый размер графа возрастает по мере роста сложности рабочей нагрузки, размера базы данных и числа разделов.
Интуитивно ясно, что для более сложной рабочей нагрузки требуется тщательно моделировать большее число транзакций (и тем самым дуг). Для базы данных большего размера в графе требуется больше вершин (кортежей). Требуется и больше дуг (т.е. больше транзакций), чтобы в графе правильно отражалось то, как производится доступ к данным. Наконец, чем больше разделов, тем более плотным должен быть граф (больше дуг). К сожалению, для формализации всего этого в виде количественной модели требуется более полный набор примеров, и такая работа находится за рамками данной статьи. Простая стратегия выбора степени сэмплинга состоит в том, чтобы пропускать нашу систему над образцами увеличивающегося размера до тех пор, пока качество разделения не перестанет повышаться. В наших простых примерах эта стратегия привела к хорошим результатам.
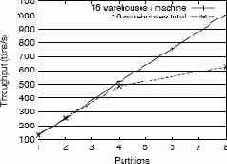
Рис. 6. Масштабируемость пропускной способности TPC-C.
