Сопряженные градиенты

Здесь мы обсуждаем параллельную по данным реализацию метода сопряженных градиентов (Conjugate Gradiant) для решения системы линейных уравнений. Мы можем использовать это для реализации машины опорных векторов (Support Vector Machines, SVM) – современного метода бинарной классификации. Бинарные классификаторы являются распространенным средством в области размещения рекламы, используемым для превращения мгогомерных характеристик пользователей в простые булевские метки типа "является любителем автомашин", которые можно объединять в диаграммы любителей (enthusiast chart). Кроме того, что метод сопряженных градиентов служит строительным блоком для SVM, он позволяет оптимизировать большой класс функций, которые можно аппроксимировать рядами Тейлора второго порядка.

Для математика решение матричного уравнения Ax = b не представляет труда, если оно существует: x = A-1b. Как отмечалось в подразделе 5.1, мы не можем считать, что в состоянии найти A-1. Если матрица A является (n × n)-симметричной и положительно определенной (symmetric and positive definite, SPD), то мы можем использовать метод сопряженных градиентов. Для применения этого метода не требуется ни df(y), ни A-1, и он сходится не более чем за n итераций. Общее описание метода проводится в . Здесь мы кратко описываем решение уравнения Ax = b как точки экстремума f(x) = ½x´Ax + b´x + c. Грубо говоря, у нас имеется некоторая оценка

нашего решения x*. Поскольку

– это всего лишь оценка,

является ненулевым. Вычитание этой ошибки r0 из оценки позволяет нам сгенерировать ряд

ортогональных векторов. Решением будет x* = Σiαipi для αi, определяемого ниже. Вычисления завершаются в точке

для соответствующего ε. Имеется несколько вариантов этого алгоритма; мы написали свой вариант в матричной нотации.

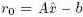
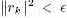
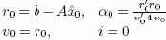
Начнем итерацию по i.

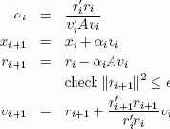
При включении этого метода в базу данных мы сохраняли (vi, xi, ri, αi) как строку и вставляли на каждом проходе строку i+1.
Для этого потребовалось определить функции update_alpha(r_i, p_i, A), update_ x(x_i, alpha_i, v_i), update_r(x_i, alpha_i, v_i, A) и update_v(r_i, alpha_ i, v_i, A). Хотя вызовы функций были избыточными (например, update_v() также запускается для обновления ri+1), это позволяло нам вставлять на каждом шаге одну полную строку. Затем перед продолжением вычислений внешний управляющий процесс проверял значение ri. После достижения точки сходимости x* вычисляется элементарным образом.

Наличие метода сопряженных градиентов позволяет реализовать более сложные методы типа SVM. В своей основе метод SVM направлен на максимизацию расстояния между заданным множеством точек и подходящей гиперплоскостью. Это расстояние выражается длиной нормальных векторов

. В большинстве методов в качестве индикаторов c используются целые числа {0, 1}, так что проблема выражается следующим образом:

при условии c´w - b ≥ 0.

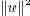
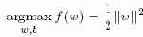
Этот метод применяется для решения более общей проблемы функций высокой размерности в приближении рядом Тейлора fx0(x) ≈ f(x0 + df(x)(x - x0) + ½(x - x0)´d2f(x)(x - x0). При хорошем начальном приближении для x* и распространенном предположении о непрерывности f(·) мы знаем, что матрица будет SPD поблизости от x*. Подробности см. в .

Содержание раздела