Обычный метод наименьших квадратов
Мы начнем с обычного метода наименьших квадратов (Ordinary Least Squares, OLS) – классического метода подбора кривой для данных, обычно с использованием полиномиальной функции. В Web-рекламе одним из стандартных приложений этого метода является моделирование сезонных тенденций. При наличии нескольких простых определенных пользователями функций над векторами аналитики могут естественным образом выражать OLS на SQL.
В нашем случае мы находим стастистическую оценку β*, наилучшем образом удовлетворяющую соотношение Y = Xβ. Здесь X = n × k – это набор фиксированных (независимых) переменных, и Y – набор из n наблюдений (зависимых переменных), которые мы хотим промоделировать посредством функции X с параметром β.
Как отмечается в ,
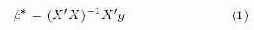
можно подсчитать путем вычисления A = X′X и b = X′y как суммирования. В параллельной базе данных это можно выполнить путем параллельного вычисления локальных A и b в каждом разделе базы данных с последующим слиянием промежуточных результатов в заключительном последовательном вычислении.
В результате будут получены квадратная матрица и вектор. Заключительное вычисление производится путем обращения небольшой матрицы A и ее умножения на вектор для получения коэффициентов β*.
Кроме того, попутно может быть произведено вычисление коэффициента смешанной корреляции R2:
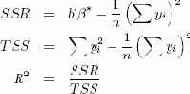
В следующем SQL-запросе мы вычисляем коэффициенты β*, а также компоненты коэффициента смешанной корреляции:
CREATE VIEW ols AS SELECT pseudo_inverse(A) * b as beta_star, (transpose(b) * (pseudo_inverse(A) * b) - sum_y2/count) -- SSR / (sum_yy - sumy2/n) -- TSS as r_squared FROM ( SELECT sum(transpose(d.vector) * d.vector) as A, sum(d.vector * y) as b, sum(y)^2 as sum_y2, sum(y^2) as sum_yy, count(*) as n FROM design d ) ols_aggs;
Отметим использование определяемой пользователем функции для транспонирования вектора и определяемых пользователем агрегатов для суммирования объектов (многомерного) массива. Массив A – это небольшой массив, размещаемый в основной памяти, с которым мы обращаемся, как с одним объектом; функция pseudo-inverse реализует известное из учебников псевдообращение матрицы методом Мура-Пенроуза (Moore-Penrose).
Все указанные вычисления можно эффективно произвести за один проход по данным. Для удобства мы инкапсулировали это еще в двух определяемых пользователями функциях:
SELECT ols_coef(d.y, d.vector), ols_r2(d.y, d.vector) FROM design d;
До выполнения реализации этой функциональности внутри СУБД один из заказчиков Greenplum имел привычку вычислять OLS путем экспорта данных и их импорта в R, и этот процесс занимал несколько часов. Они сообщали о значительном повышении производительности после перехода к вычислению внутри СУБД. Основным преимуществом является параллельное выполнение анализа неподалеку от данных с их минимальным перемещением.
