Логарифмические отношения правдоподобия

Отношения правдоподобия полезны для сравнения некоторой подсовокупности с совокупностью в целом по некоторым конкретным характеристикам. Например, в области рекламы могут учитываться такие характеристики пользователей, как любимый напиток и семейное положение. Могло бы потребоваться узнать, привлекает ли кофе молодых родителей в большей степени, чем популяцию в целом.

Здесь мы имеем две функции плотности (или распределения масс) для одного и того же набора данных X. Назовем одно распределение основной гипотезой f0, а другое – альтернативной гипотезой f1. Обычно f0 и f1 являются разными параметризациями одной и той же плотности. Например, N(μ0, σ0) и N(μA, σA). Сходство L относительно fi задается следующим соотношением:

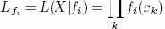
Логарифмическое отношение подобия (log-likelihood ratio, LLR) определяется как

Взятие логарифма позволяет нам использовать хорошо известную χ2-аппроксимацию для больших n. Кроме того, произведения приятным образом превращаются в суммы, и РСУБД может легко производить вычисления параллельно.

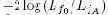
Эти вычисления хорошо распределяются, если

а в большинстве случаев это именно так. Если же

то к работе с векторами как с распределенными объектами нужно относиться с осторожностью. Предположим, что значения содержатся в таблице T, и что функция fA(·) реализована как определяемая пользователями функция f_llk(x numeric, param numeric). Тогда все вычисление может быть произведено посредством вызова

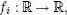
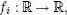
SELECT 2 * sum(log(f_llk(T.value, d.alt_param))) - 2 * sum(log(f_llk(T.value, d.null_param))) AS llr FROM T, design AS d

Для вычисления такого запроса от РСУБД требуется значительная гибкость и изощренность.

Пример: полиномиальное распределение

Полиномиальное (multinomial) распределение является расширением биномиального распределения. Рассмотрим случайную переменную X с k дискретными исходами. Для них имеются вероятности p = (p1, ...,pk1). При n попытках суммарное распределение вероятности выражается следующим образом:

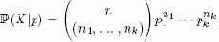
Чтобы получить pi, предположим, что базисная совокупность представлена в таблице outcome со столбцом outcome.

CREATE VIEW B AS SELECT outcome, outcome_count / sum(outcome_count) over () AS p FROM (SELECT outcome, count(*)::numeric AS outcome_count FROM input GROUP BY outcome) AS a

В контексте выбора модели часто бывает удобно сравнить один и тот же набор данных при наличии двух разных полиномиальных распределений.

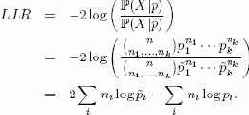
Или на SQL:

SELECT 2 * sum(T.outcome_count * log B.p) - 2 * sum(T.outcome_count * log T.p) FROM B, test_population AS T WHERE B.outcome = T.outcome

Содержание раздела