Декомпозиция метода (основные фазы)
Хотя не все системы вывода, основанного на прецедентах, полностью включают этапы, приведенные ниже (Рис. 1), подход, основанный на прецедентах, в целом состоит из следующих компонентов [Aamodt 94]:
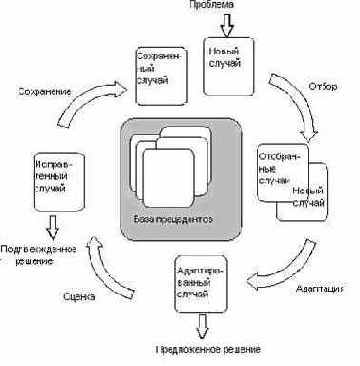
Рис 1. Цикл вывода на основе прецедентов
Проблема выбора подходящего прецедента является одной из самых важных в таких системах. Естественно искать подходящий прецедент в той области пространства поиска, где находятся решения сходных проблем, иначе говоря, поиск должен быть организован сообразно цели. Но как определить, какие именно решения считать сходными?
Эффективность поиска прецедентов для текущего случая во многом зависит от того, по каким признакам организован индекс в базе прецедентов. Это, в свою очередь, требует хороших знаний о предметной области и конечной цели решения проблемы. Однако выбор наилучшего индекса не может быть столь же прост, как это звучит, так как не имеется никаких общих рекомендаций для этого. Для ориентира, однако, можно привести четыре свойства хороших индексов [Kolodner 83]:
После того, как прецеденты извлечены, нужно выбрать "наиболее подходящий" из них. Это определяется сравнением признаков текущего случая и выбранных прецедентов. Определение метода, на котором будет основываться нахождение меры сходства прецедентов, решается во время создания системы ее разработчиками. Наиболее популярным и часто используемым является метод "ближайшего соседа" (nearest neighbour) [Anand 99].
В его основе лежит тот или иной способ измерения степени близости прецедента и текущего случая по каждому признаку (будь это текстовый, числовой или булевский), который пользователь сочтет полезным для достижения цели.
Говоря более строгим языком, вводится метрика на пространстве всех признаков, в этом пространстве определяется точка, соответствующая текущему случаю, и в рамках этой метрики находится ближайшая к ней точка из точек, представляющих прецеденты. Описанный здесь алгоритм очень прост – реально применяются некоторые его модификации. Обычно прогноз делается на основе нескольких ближайших точек, а не одной (K-nearest neighbours). Такой метод более устойчив, поскольку позволяет сгладить отдельные выбросы, случайный шум, всегда присутствующий в данных.
Каждому признаку назначают вес, учитывающий его относительную ценность. Полностью степень близости прецедента по всем признакам можно вычислить, используя обобщенную формулу вида:


где wj – вес j-го признака, sim – функция подобия (метрика), xij и xik – значения признака xj для текущего случая и прецедента, соответственно. После вычисления степеней близости все прецеденты выстраиваются в единый ранжированный список.
Метод прост, он может быть реализован очень эффективно, правда требует для работы большой памяти, так как в процессе нахождения значения зависимой переменной для новой записи используется вся существующая база данных.
Выбор метрики (или меры близости) считается узловым моментом, от которого решающим образом зависит поиск подходящих прецедентов. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т. п. В некоторых методах выбор метрики достигается с помощью специальных алгоритмов преобразования исходного пространства признаков.
Пусть имеются образцы Xi и Xk в N-мерном пространстве признаков. Основные метрики, традиционно используемые при выборе прецедентов, приводятся в таблице 1.
После того, как выбран подходящий прецедент, при поиске решения для целевой проблемы выполняется адаптация – модификация имеющегося в нем решения с целью его оптимизации.
Невозможно выработать единый вариант для такой адаптации, так как это в большой степени зависит от предметной области. Если существуют алгоритмы адаптации, они обычно предполагают наличие зависимости между признаками прецедентов и признаками содержащихся в них решений. Такие зависимости могут задаваться человеком при построении базы прецедентов или обнаруживаться в базе автоматически.
Процесс модификации решения при его адаптации к текущему случаю может включать ряд шагов, от простой замены некоторых компонентов в имеющемся решении, корректировки или интерполяции (числовых) признаков или изменения порядка операций, до более существенных. Имеются и другие подходы:
- Повторная конкретизация переменных в существующем прецеденте и присвоение им новых значений.
- Уточнение параметров. Некоторые прецеденты могут содержать числовые значения, например, время выполнения какого-либо этапа плана. Это значение должно быть уточнено в соответствии с новым значением другого свойства.
- Поиск в памяти. Иногда требуется найти способ преодоления затруднения, возникшего как побочный эффект замены одних компонентов решения другими.
Обратная связь, возникающая при сохранении решений для новых проблем, означает, что вывод по прецедентам по своей сути является "самообучающейся" технологией, благодаря чему рабочие характеристики каждой базы прецедентов с течением времени и накоплением опыта непрерывно улучшаются. Разработка баз прецедентов по конкретной проблеме или области деятельности происходит на естественном (русском, английском) языке, то есть не требует никакого программирования, и может быть выполнена наиболее опытными сотрудниками – экспертами, работающими в данной конкретной области.
Не стоит, однако, рассчитывать, что экспертная система будет действительно принимать решения. Принятие решения всегда остается за человеком, а система лишь предлагает несколько возможных вариантов и указывает на самый "разумный" из них с ее точки зрения.
| Наименование метрики | Тип признаков | Формула для оценки меры близости (метрики) |
| Эвклидово расстояние | Количественные | 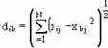 |
| Манхэттенская метрика | Количественные | 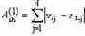 |
| Мера сходства Хэмминга | Номинальные (качественные) | 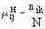 где nik – число совпадающих признаков у образцов Xi и Xk. |
| Мера сходства Роджерса-Танимото | Номинальные шкалы | 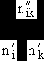 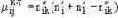 где – число совпадающих единичных признаков у образцов Xi и Xk; , – общее число еди-ничных признаков у образцов Xi и Xk соответственно. |
| Расстояние Махалонобиса | Количественные | 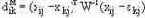 W – ковариационная матрица выборки 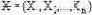 |
| Расстояние Журавлева | Смешанные | 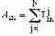 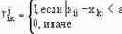 |
