Байесовские сети
Байесовские сети (Bayesian Networks) – это статистический метод описания закономерностей в данных. На основе первичной информации, содержащейся в базах данных, строится модель в виде сети, где множество вершин описывает события, а ребра интерпретируются как причинные связи между событиями.
В основе байесовских сетей лежит теорема Байеса теории вероятностей для определения апостериорных вероятностей попарно несовместных событий Yi по их априорным вероятностям:
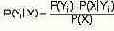
Всякое множество ребер, представляющее собой все пути между некоторыми двумя вершинами, соответствует условной зависимости между этими вершинами. Если задать некоторое распределение вероятностей на множестве переменных, соответствующих вершинам этого графа, то полученная сеть будет называться байесовской сетью. На такой сети можно использовать, так называемый байесовский вывод для вычисления вероятностей следствий событий.
Критерий отбора прецедентов заключается в следующем. Если нет полностью совпадающего прецедента, вычисляется распределение вероятностей по тем признакам, которые не совпадают с признаками текущего случая. Выбирается тот прецедент, для которого эта вероятность наибольшая.
Существуют два способа обучения байесовских сетей с помощью прецедентов: уточнение параметров сети, если структура сети известна, и выбор из множества моделей, применяя введенную метрику ко всей базе прецедентов.
Экерман [Heckerman 97] отмечает четыре достоинства байесовских сетей как средства извлечения данных:
- поскольку в модели определяются зависимости между всеми переменными, легко обрабатываются ситуации, когда значения некоторых переменных неизвестны;
- построенные байесовские сети просто интерпретируются и позволяют на этапе прогностического моделирования легко производить анализ по сценарию "что если…";
- подход позволяет естественным образом совмещать закономерности, выведенные из данных, и фоновые знания, полученные в явном виде, например, от экспертов;
- использование байесовских сетей позволяет избежать проблемы переподгонки (overfitting), то есть избыточного усложнения модели, чем страдают многие методы (например, деревья решений и индукция правил) при слишком буквальном следовании распределению зашумленных данных.
Несмотря на свою простоту, скорость и интерпретируемость результатов, наивно-байесовский алгоритм имеет недостатки:
- перемножать условные вероятности корректно только тогда, когда все входные переменные действительно статистически независимы; допущение этой независимости и обуславливает уточнение "наивно-" в названии алгоритма, хотя, по приведенным в [Brand 98/2] примерам он показывает неплохие практические результаты даже при несоблюдении условия статистической независимости; корректно данная ситуация обрабатывается только более сложными методами, основанными на обучении байесовских сетей [Heckerman 95, Heckerman 97];
- невозможна непосредственная обработка непрерывных переменных – их требуется разбивать на множество интервалов, чтобы атрибуты были дискретными; такое разбиение в ряде случаев приводит к потере значимых закономерностей [Brand 98/2];
- наивно-байесовский подход учитывает только индивидуальное влияние входных переменных на результат классификации, не принимая во внимание комбинированного влияния пар или троек значений разных атрибутов [Brand 98/2], что было бы полезно с точки зрения прогностической точности, но значительно увеличило бы количество проверяемых комбинаций.
Байесовские сети активно использовались для формализации знаний экспертов в экспертных системах [Heckerman 95], но с недавних пор стали применяться для извлечения знаний из наборов данных. Приведем несколько примеров систем, в которых используется интеграция байесовских сетей и вывод по прецедентам.
Компания Microsoft разработала прототип системы для диагностики неисправностей с кодовым именем ALADDIN [Breese 95]. В системе используется трехуровневая байесовская сеть. Первый уровень описывает одну или несколько причин – факторов, приведших к сбою, второй – результат, который будет получен при наличии всех причин, и третий – симптомы, вызываемые результатом. Байесовская сеть конструируется экспертом и корректируется при каждом использовании. Microsoft прекратила использование системы в связи с малым объемом базы знаний.
В Университете Salford’а [Rodriguez 97], была разработана система, в которой одна байесовская сеть используется для индексации категорий – групп прецедентов, объединенных по принципу общности свойств, а другая – для индексации экземпляров, то есть единичных прецедентов внутри категории.
INBANCA [Aha 96] – система, разработанная Центром Прикладных Исследований ВМС США для принятия плана действий, адекватных текущей ситуации. Байесовская модель используется при описании окружающей среды.
D-SIDE [Tirri 96] – это программный пакет, разработанный в Университете Хельсинки. Здесь прецеденты рассматриваются как вектора. Допускается, что база может иметь некорректные прецеденты. Байесовская модель используется при адаптации решения прецедента к текущему случаю, в частности, для предсказания наиболее вероятных значений отсутствующих признаков.
Существующие системы используют разные подходы. Первые две используют добычу данных для выявления знаний о предметной области. INBANCA использует прецеденты для выбора плана действий, ALADDIN использует прецеденты для устранения ошибки, найденной с помощью байесовских сетей, система в Salford’е использует байесовские сети для манипулирования прецедентами, и, наконец, D-SIDE использует прецеденты для классификации.
